GMAT Hard Math Questions | PS
GMAT Problem Solving | 700 800 Level Questions
GMAT 700 Level Sample Question in Algebra / Inequalities
If x is a positive integer such that (x-1)(x-3)(x-5)....(x-93) < 0, how many values can x take?
700 800 Level GMAT Sample Question | Probability
If two distinct integers a and b are picked from {1,2,3,4....100} and multiplied, what is the probability that the resulting number has EXACTLY 3 factors?
- \\frac{4}{25 \times 99})
- \\frac{2}{25 \times 99})
- \\frac{8}{25 \times 99})
- \\frac{16}{25 \times 99})
- \\frac{32}{25 \times 99})
700 800 Level GMAT Word Problem | Rates Problem Solving Question
Working alone, A can complete a task in 'a' days and B in 'b' days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task in exactly 10 days. If B starts, they take half a day more. How long does it take to complete the task if they both work together?
- \\frac{46}{9})
- \\frac{50}{9})
- \\frac{50}{11})
- \\frac{36}{7})
- \\frac{210}{41})
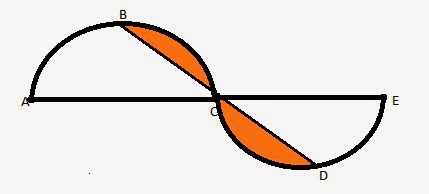
GMAT 700 800 Level Question | Geometry | Area of Circles
In the figure given below, ABC and CDE are two identical semi-circles of radius 2 units. B and D are the mid points of the arc ABC and CDE respectively. What is the area of the shaded region?
![semicircle]()
GMAT Hard Math Questions | Algebra | Absolute Values Sample Question
If a, b, and c are not equal to zero, what is the difference between the maximum and minimum value of S?
\\ S = 1+\frac { \left| a \right| }{ a } +\frac {2 \left| b \right| }{ b } +\frac {3 \left| ab \right| }{ ab } -\frac {4 \left| c \right| }{ c } \\)
GMAT 700 Level Sample Question in Statistics
Consider a set S = {2, 4, 6, 8, x, y} with distinct elements. If x and y are both prime numbers and 0 < x < 40 and 0 < y < 40, which of the following MUST be true?
I. The maximum possible range of the set is greater than 33.
II. The median can never be an even number.
III. If y = 37, the average of the set will be greater than the median.- I only
- I and II only
- I and III only
- III only
- I, II and III
GMAT Hard Math Algebra - Absolute Values | GMAT Problem Solving
If x and y are integers and |x - y| = 12, what is the minimum possible value of xy?
GMAT Challenging Question | Statistics Problem Solving
Three positive integers a, b, and c are such that their average is 20 and a ≤ b ≤ c. If the median is (a + 11), what is the least possible value of c?
GMAT Hard Math | Arithmetic | Permutation Combination Sample Question
How many four-digit positive integers exist that contain the block 25 and are divisible by 75. (2250 and 2025 are two such numbers)?
700 800 Level GMAT Word Problem | Number Properties & Equations Problem Solving Question
A movie hall sold tickets to one of its shows in two denominations, $11 and $7. A fourth of all those who bought a ticket also spent $4 each on refreshments at the movie hall. If the total collections from tickets and refreshments for the show was $124, how many $7 tickets were sold? Note: The number of $11 tickets sold is different from the number of $7 tickets sold.
GMAT 700 800 Level Question | Coordinate Geometry & Permutation Combination
Rectangle ABCD is constructed in the xy-plane so that sides AB and CD are parallel to the x-axis. Both the x and y coordinates of all four vertices of the rectangle are integers. How many rectangles can be constructed if x and y coordinates satisfy the inequality 11 < x < 29 and 5 ≤ y ≤ 13?
GMAT Hard Math Question | Algebra | Difficult Equations Question
Susan invited 13 of her friends for her birthday party and created return gift hampers comprising one each of $3, $4, and $5 gift certificates. One of her friends did not turn up and Susan decided to rework her gift hampers such that each of the 12 friends who turned up got $13 worth gift certificates. How many gift hampers did not contain $5 gift certificates in the new configuration?
GMAT 700 Level Sample Question in Counting Methods
149 is a 3-digit positive integer, product of whose digits is 1 × 4 × 9 = 36. How many 3-digit positive integers exist, product of whose digits is 36?
GMAT Hard Math Arithmetic | Permutation Combination - Selections | GMAT Problem Solving
A student is required to solve 6 out of the 10 questions in a test. The questions are divided into two sections of 5 questions each. In how many ways can the student select the questions to solve if not more than 4 questions can be chosen from either section?
GMAT 700 800 Level Question | Arithmetic | Counting Methods Problem Solving
How many 6-digit numbers can be formed using the digits {1, 2, 3, ... 9} such that any digit that appears in such a number appears at least twice?
GMAT Hard Math | Arithmetic | Number Properties Sample Question
If y is the highest power of a number 'x' that can divide 101! without leaving a remainder, then for which among the following values of x will y be the highest?
GMAT 650 Level Algebra Question | Polynomials
If a, b, .. , j are real numbers such that (a - 1)2 + (b - 2)4 + (c - 3)6 + ... + (j - 10)20 = 0, what is the value of b × d × f × h × j?
GMAT Hard Math Arithmetic - Counting Methods | GMAT Problem Solving
What is the sum of all 3-digit positive integers such that all the digits of each of the number is even?
GMAT Challenging Math Question | Arithmetic | Number Properties - Remainders
What is the least number that when divided by 44 leaves a remainder 31, when divided by 56 leaves a remainder 43, and when divided by 32 leaves a remainder 19?
GMAT Number Properties Practice | 650 Level Question | Factors Problem Solving
What is the product of all the factors of the cube of a positive integer 'n' if the product of all the factors of square of n is n3?
GMAT Arithmetic Question | Numbers Counting Methods Problem Solving
How many even 3-digit positive integers with distinct digits are there?
GMAT Algebra Practice Question | Equations & Numbers PS
If x and y are non-negative integers such that 4x + 7y = 68, how many values are possible for (x + y)?
GMAT Sample Questions | Topicwise GMAT Questions
Copyrights © 2016 - 26 All Rights Reserved by Wizako.com - An Ascent Education Initiative.
Privacy Policy | Terms & Conditions
GMAT® is a registered trademark of the Graduate Management Admission Council (GMAC). This website is not endorsed or approved by GMAC.
GRE® is a registered trademarks of Educational Testing Service (ETS). This website is not endorsed or approved by ETS.
SAT® is a registered trademark of the College Board, which was not involved in the production of, and does not endorse this product.
How to reach Wizako?
Mobile: (91) 95000 48484
WhatsApp: WhatsApp Now
Email: [email protected]
Leave A Message