GMAT Challenging Question 8 | Geometry - Triangles & Semicircles

The given question is a GMAT 700 level Geometry Problem Solving question. The core concept that is tested in this GMAT sample question is segregating the area of the semi circle into parts so that the area of the shaded region can be found.

Question 8: In the figure given below, ABC and CDE are two identical semi-circles of radius 2 units. B and D are the mid points of the arc ABC and CDE respectively. What is the area of the shaded region?

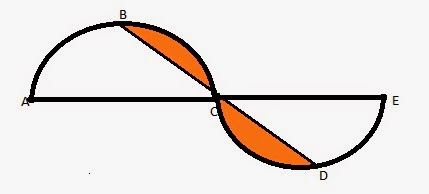
1. 4π - 1
2. 3π - 1
3. 2π - 4
4. \\frac{\text{1}}{\text{2}}) (3π - 1)
5. 2π - 2

Video Explanation

Explanatory Answer | GMAT Geometry - Triangles and circles.

Step 1: Divide each semicircle into a triangle and the shaded region

P and Q are the centers of the two semicircles.
Draw BP perpendicular to AC.

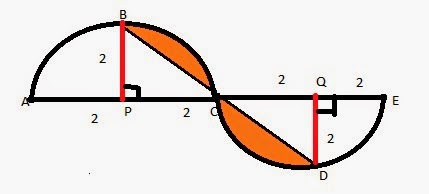
BP is radius to the semi-circle. So are AP and PC.
Therefore, BP = AP = PC = 2 units.
In semicircle ABC, area of the shaded portion is the difference between the area of half the semicircle PBC and the area of the triangle PBC.
Triangle PBC is a right triangle because PB is perpendicular to PC. PB and PC are radii to the circle and are equal. So, triangle PBC is an isosceles triangle.
Therefore, triangle PBC is a right isosceles triangle.

Step 2: Compute areas of half the semicircle and the triangle

Area of half the semicircle − Area of region PBC

Area of the semicircle ABC = \\frac{\text{1}}{\text{2}}) area of the circle of radius 2.
So, area of half the semicircle, PBC = \\frac{\text{1}}{\text{4}}) area of the circle of radius 2.
Area of half the semicircle, PBC = \\frac{\text{1}}{\text{4}}) × π × 2²
Area of half the semicircle, PBC = π sq units

Area of right isosceles triangle PBC

Area of right triangle PBC = \\frac{\text{1}}{\text{2}}) × PC × PB
Area of triangle PBC = \\frac{\text{1}}{\text{2}}) × 2 × 2 = 2 sq units

Area of shaded region

Area of shaded region in one of the semi circles ABC = (π - 2) sq units
Therefore, area of the overall shaded region = 2(π - 2) sq units = 2π - 4 sq units

Choice C is the correct answer.