GMAT 700 800 Quant Question 18

The given question is a challenging GMAT 700 800 level quant problem solving question combining concepts in coordinate geometry and permutation combination. A very interesting and challenging GMAT hard math question.

Question 18: Rectangle ABCD is constructed in the xy-plane so that sides AB and CD are parallel to the x-axis. Both the x and y coordinates of all four vertices of the rectangle are integers. How many rectangles can be constructed if x and y coordinates satisfy the inequality 11 < x < 29 and 5 ≤ y ≤ 13?

1. 153
2. 153C₄
3. 4896
4. 2448
5. 5508

Video Explanation

Explanatory Answer | GMAT Geometry Practice

KeyData

Sides AB and CD are parallel to x-axis.
So, AD and BC will be parallel to y-axis.

The x-coordinates take values from 12 to 28.
We can draw lines parallel to y-axis corresponding to each of these values.
So, we will be able to draw 17 vertical lines.

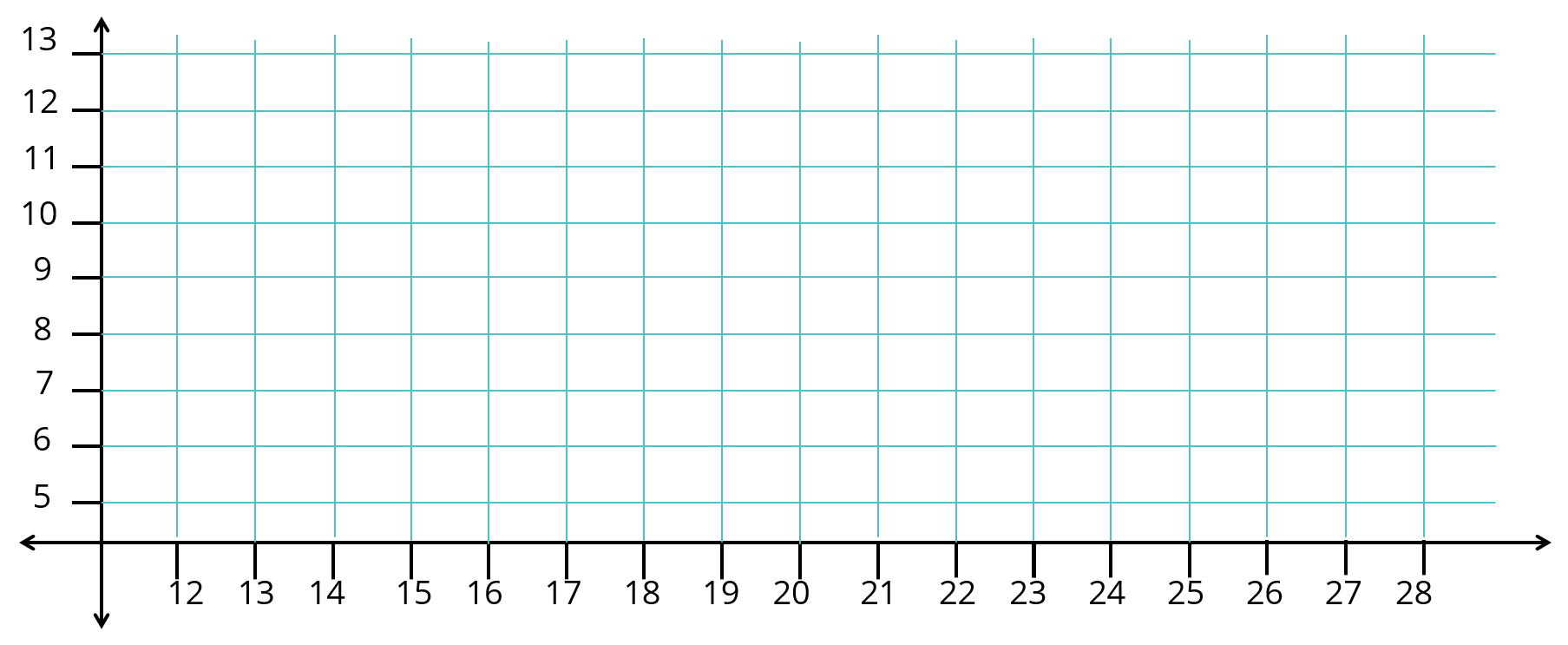
The y-coordinates take values from 5 to 13.
We can draw lines parallel to x-axis corresponding to each of these values.
So, we will be able to draw 9 horizontal lines.

Key Question: What maketh a rectangle?

2 horizontal lines and two vertical lines will form a rectangle
Number of ways of selecting 2 horizontal lines from 9 horizontal lines = 9C₂
9C₂ = \\frac{9 × 8}{2}) = 36

Number of ways of selecting 2 veritcal lines from 17 vertical lines = 17C₂
9C₂ = \\frac{17 × 16}{2}) = 136

Number of rectangles that can be formed

Product of the number of ways of selecting 2 horizontal lines and number of ways of selecting two vertical lines
= 36 × 136 = 4896

Choice C is the correct answer.